Нужно пересчитать координаты вектора при переходе из одной системы координат в другую. Нам заданы матрицы трансформации в виде вектора — переноса начала координат и углов поворота относительно осей.

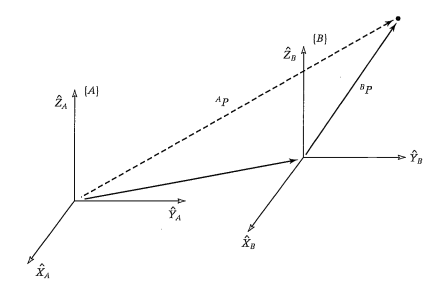
Исходные данные:

• Вектор в исходной системе координат: (x, y, z) (предположим, что это вектор-столбец)
• Вектор переноса начала координат (translation vector): (Tx, Ty, Tz) - задает смещение нового начала координат относительно старого
• Углы поворота (rotation angles): α (вокруг оси X), β (вокруг оси Y), γ (вокруг оси Z) (ZYX порядок поворотов)

(Важно! Порядок поворотов имеет значение).

Шаги для пересчета координат:

1. Поворот (Rotation):

   Сначала необходимо повернуть вектор (x, y, z) в соответствии с углами поворота. Для этого необходимо создать матрицу поворота (Rotation Matrix).

   Матрица поворота вокруг оси X (Rx):

   \(\begin{bmatrix} 1 & 0 & 0 \\ 0 & \cos(\alpha) & -\sin(\alpha) \\ 0 & \sin(\alpha) & \cos(\alpha) \end{bmatrix}\)

   Матрица поворота вокруг оси Y (Ry):

   \(\begin{bmatrix} \cos(\beta) & 0 & \sin(\beta) \\ 0 & 1 & 0 \\ -\sin(\beta) & 0 & \cos(\beta) \end{bmatrix}\)

   Матрица поворота вокруг оси Z (Rz):

   \(\begin{bmatrix} \cos(\gamma) & -\sin(\gamma) & 0 \\ \sin(\gamma) & \cos(\gamma) & 0 \\ 0 & 0 & 1 \end{bmatrix}\)

   Общая матрица поворота R (ZYX): R = Rz * Ry * Rx

   "Повернутый" вектор:

$$ \textit{v_rotated} = R*(x, y, z) $$

2. Перенос (Translation):

   После поворота необходимо учесть перенос начала координат. Вектор (Tx, Ty, Tz) указывает смещение нового начала координат относительно старого.

   $$ \textit{v_new} = \textit{v_rotated} - (Tx, Ty, Tz)$$

Итого, что мы должны сделать:

Порядок расчетов:

1. Рассчитываем матрицы поворотов по осям:
   • Rx:
     \(\begin{bmatrix} 1 & 0 & 0 \\ 0 & \cos(\alpha) & -\sin(\alpha) \\ 0 & \sin(\alpha) & \cos(\alpha) \end{bmatrix}\)
   • Ry:
     \(\begin{bmatrix} \cos(\beta) & 0 & \sin(\beta) \\ 0 & 1 & 0 \\ -\sin(\beta) & 0 & \cos(\beta) \end{bmatrix}\)
   • Rz:
     \(\begin{bmatrix} \cos(\gamma) & -\sin(\gamma) & 0 \\ \sin(\gamma) & \cos(\gamma) & 0 \\ 0 & 0 & 1 \end{bmatrix}\)
2. Рассчитываем общую матрицу поворота: R = Rz * Ry * Rx
3. Поворачиваем вектор (находим его координаты если бы при этом он оставался в текущей системе координат): v_rotated = R * [x, y, z]
4. Переносим координаты повернутого вектора с поправкой на то, что начало координат также изменилось: v_new = v_rotated - [Tx, Ty, Tz]

Пример на Python (используем NumPy):

import numpy as np
import math

def transform_coordinates(x, y, z, Tx, Ty, Tz, alpha_deg, beta_deg, gamma_deg):
    """
    Пересчитывает координаты вектора из одной системы координат в другую.

    Args:
        x, y, z: Координаты вектора в исходной системе координат.
        Tx, Ty, Tz: Вектор переноса начала координат.
        alpha_deg, beta_deg, gamma_deg: Углы поворота в градусах (ZYX порядок).

    Returns:
        (x_new, y_new, z_new): Координаты вектора в новой системе координат.
    """
    # Преобразуем углы в радианы
    alpha = math.radians(alpha_deg)
    beta = math.radians(beta_deg)
    gamma = math.radians(gamma_deg)

    # Матрицы поворотов
    Rx = np.array([[1, 0, 0],
                   [0, math.cos(alpha), -math.sin(alpha)],
                   [0, math.sin(alpha), math.cos(alpha)]])

    Ry = np.array([[math.cos(beta), 0, math.sin(beta)],
                   [0, 1, 0],
                   [-math.sin(beta), 0, math.cos(beta)]])

    Rz = np.array([[math.cos(gamma), -math.sin(gamma), 0],
                   [math.sin(gamma), math.cos(gamma), 0],
                   [0, 0, 1]])

    # Общая матрица поворота (ZYX)
    R = Rz @ Ry @ Rx

    # Преобразуем исходный вектор в вектор-столбец
    v_original = np.array([x, y, z])

    # Поворачиваем вектор
    v_rotated = R @ v_original

    # Переносим вектор
    v_new = v_rotated - np.array([Tx, Ty, Tz])

    return tuple(v_new)


# Пример использования:
x = 2
y = 3
z = 4
Tx = 1
Ty = 2
Tz = 3
alpha_deg = 30  # Угол поворота вокруг X (в градусах)
beta_deg = 45   # Угол поворота вокруг Y (в градусах)
gamma_deg = 60  # Угол поворота вокруг Z (в градусах)


x_new, y_new, z_new = transform_coordinates(x, y, z, Tx, Ty, Tz, alpha_deg, beta_deg, gamma_deg)
print(f"Исходные координаты: ({x}, {y}, {z})")
print(f"Новые координаты: ({x_new:.2f}, {y_new:.2f}, {z_new:.2f})")

На выходе получим новые координаты вектора:

Исходные координаты: (2, 3, 4)
Новые координаты: (0.94, 2.56, -0.90)